
朴素贝叶斯分类器
一,生成词向量(词集模型)
第一,假设这里有两个参数vocabList, inputSet。vocabList代表着包含很多无重复的词,词量足够大,inputSet代表着我们预转换的词列表。第二,创建一个与vocabList列表等长的全0列表returnVec,用于保存我们后面inputSet里中词是否存在vocabList的标记。如果存在,则在对应为置为1;如果不存在,这里简单处理直接忽略。因此尽量使vocabList里的词足够多。遍历inputSet词列表,针对每一个元素检测是否出现在vocabList列表中,存在,则在与vocabList同一索引处的returnVec列表中置位置上中置1,代完成词向量标记处理。第三,返回returnVec列表即可。 def setOfWords2Vec(vocabList, inputSet): returnVec = [0] * len(vocabList) for word in inputSet: if word in vocabList: returnVec[vocabList.index(word)] = 1 else: print "the %s word not in vocabList" % word return returnVec
这是词集模型,即将词的出现与否作为统计度量,如果一个词多次出现与出现一次是一样的;而词袋,还包含了词出现的次数。在程序中只需修改为returnVec[vocabList.index(word)] += 1

贝叶斯概率.png
如果在贝叶斯定理中涉及多个属性,我们需要假设这些属性间中相互独立的,也即一个属性的出现与否不受其他属性的影响,虽然假设是不一定成立的,但这也正是朴素二字的体现。相比硬规则而言,这已经使朴素贝叶斯分类器具有相当好的结果了。图贝叶斯公式很容易由训练集求得P(X1|Ci)、P(X2|Ci)、P(X3|Ci)...P(Xn|Ci)概率。X k表示元组X在属性A k的值。对于每个属性需要考查属性值是分类属性还是连续值属性。(1)如果是分类属性,则P(X1|Ci)的值由属性值为X1的元组的属于Ci类别的元组与所有属于Ci的元组相比求得。(2)如果是连续值,数个P(X1|Ci)、P(X2|Ci)、P(X3|Ci)...P(Xn|Ci)的概率值乘积也不难求,通常假定Xi服从均值为u,标准差为sigma的高斯分布贝叶斯公式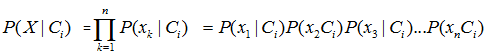
朴素贝叶斯计算公式.png
Xk服从服从均值为u,标准差为sigma的高斯分布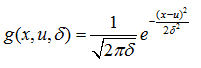
高斯计算公式.png
也即我们只需求出Ci类训练元组A k的均值及标准差即可。第二,这里做的是朴素贝叶斯分类属性的应用,两个类别,1代表着垃圾邮件,0代表正常邮件。(1)计算训练文档条数,该训练文档由词向量组成。(2)分别计算属于各个分类的词出现次数和该分类下总词数。需要计算多个概率的乘积以推测具有某些属性的词应归属于哪个类别下,如分类为1具有X1,X2,X3,Xn属性值的概率:P(X1|C=1)* P(X2|C=1)*P(X3|C=1)...P(Xn|C=1),如果其中一个概率为0,那么最终概率结果便成0了,正反例概率同时为0的概率很大,也就意味着分类无效。为降低概率为0影响,我们在开始为每个词出现次数设置为1,文档数为2。同时,为避免多个float小数相乘结果下溢问题,使用numpy模块的log函数,注意在下面程序中,我使用python自带的log函数运算失败,该用numpy才算成功。(3)计算训练文档的垃圾率,因为向量元素1代表着垃圾,故垃圾文档率为P(C1)。 def trainNB0(trainMatrix, trainCategory): numTrainDocs = len(trainMatrix) numWords = len(trainMatrix[0]) pAbusive = sum(trainCategory) / float(numTrainDocs) p0Num = ones(numWords) p1Num = ones(numWords) # p1Num 为单词出现次数数组 p0Denom = 2.0 p1Denom = 2.0 # p1Denom为数据集中总词数 for i in range(numTrainDocs): if trainCategory[i] == 1: p1Num += trainMatrix[i] p1Denom += sum(trainMatrix[i]) else: p0Num += trainMatrix[i] p0Denom += sum(trainMatrix[i]) p1Vect = log(p1Num / p1Denom) p0Vect = log(p0Num / p0Denom) return p0Vect, p1Vect, pAbusive
三, 朴素贝叶斯分类器各类别先验概率
在前面我们为避免多个小数值相乘结果下溢问题,使用了log函数相加便得出正反例概率相对值大小。P(C|W) = P(W|C) * P(C) / P(W)在计算正反例(这里仅仅有两个分类)后验概率是,由于分母P(W)代表着在所有文档中该属性组合出现的概率,它是相等的,所以,我们可以仅仅比较分子大小便可以得出具有某些特征的文档属于哪个类别。def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1): # 不在预保留的词汇表中的词语默认都是好词 # vec2Classify 用来确定测试单词是否存在。 p1 = sum(vec2Classify * p1Vec) + log(pClass1) p0 = sum(vec2Classify * p0Vec) + log(1 - pClass1) if p1 > p0: return 1 else: return 0
有一点需要注意的是,sum(vec2Classify * p1Vec) + log(pClass1)表示贝叶斯定理的分子部分。
def testingNB(): listOfPosts, listClasses = loadDataSet() myVocabList = createVocabList(listOfPosts) trainMat = [] for postinDoc in listOfPosts: trainMat.append(setOfWords2Vec(myVocabList, postinDoc)) p0V, p1V, pAb = trainNB0(array(trainMat), array(listClasses)) testEntry = ['love', 'my', 'dalmation'] thisDoc = array(setOfWords2Vec(myVocabList, testEntry)) print testEntry,"classified is:", classifyNB(thisDoc, p0V, p1V, pAb) testEntry =['beijing', 'HongKong'] thisDoc = array(setOfWords2Vec(myVocabList, testEntry)) print testEntry, "classified is:", classifyNB(thisDoc, p0V, p1V, pAb)
因为在训练数据集没有['beijing', 'HongKong'],同时对训练集中不存在的词的处理默认是非垃圾的,故在这里可以看到['beijing', 'HongKong']也被分到正常类别当中。
alist = [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9], [10, 11, 12, 13, 14], [15, 16, 17, 18, 19], [20, 21, 22, 23, 24], [25, 26, 27, 28, 29], [30, 31, 32, 33, 34], [35, 36, 37, 38, 39], [40, 41, 42, 43, 44], [45, 46, 47, 48, 49]]classes = [1, 0, 1, 1, 1, 0, 0, 1, 0, 0]trainingIndexSet = range(len(alist))testIndexSet = []for i in range(3): index = int(random.uniform(0, len(trainingIndexSet))) print 'index: ', index testIndexSet.append(trainingIndexSet[index]) del trainingIndexSet[index]print testIndexSet# 在模型训练和测试时通过`alist[trainingIndexSet[i]]`、`alist[testIndex[i]]`获取数据集
注意uniform函数按说能够返回与末端相等的值,但我试验循环1百万次没试出来。
还有一种对分类号操作的实现,这里不写了。六,总结(1)词集仅仅统计一个单词是否出现;而词袋还包含了单词出现次数的统计,相当在计算贝叶斯先验概率时为每个单词赋予权重;TF-IDF是更高级的文本分类应用,它排除了辅助词对文本分类的影响,如中文中的"的","是","啊"等词,这些词在对正确分类的贡献小、价值低,因此给予它很小的权重,虽然出现次数很多,这也就是逆文档率概念。(2)贝叶斯先验概率求解过程涉及多个概率相乘问题,最终结果可能下溢问题,故选用log,首选numpy,Python自带的log函数可能不合适。